[Note: this piece is still very much a draft, but (a) I thought it might be useful enough to the occasional person that it was worth posting, and more proximately, (b) I needed to post something for a blog-a-thon I was hosting. However, as such, it’s not quite finished and not up to my usual par. Enjoy!]

I think this piece may be especially useful for people who have always just been unexplainably “bad” or “slow” at math, but who also seem to sometimes just “get” some math conceptual stuff rock solidly well. This piece is least likely to be least helpful for people who have always been “good” at math.

I. I’m slow at math

I was always slow at math — the sort of math you do in middle- & high-school, and early college. Slow enough that I’d take twice (!!) as long on homeworks as my friends. Slow enough that practice problems were a horrible, draining, tensed process. Slow enough that studying for tests would involve reviewing the general ideas, not just doing some example problems to get the gist.

This was especially annoying because I otherwise enjoyed and was reasonably good at the abstract stuff — at grasping the underlying ideas, working through their implications, and deriving new-to-me characterizations. (In my Calc 1 class, I turned in none of the homeworks the entire semester, and studied just by explaining the concepts to my friends, then letting them work through practice problems themselves — but I aced every exam and got an A+ in the class. And when I took first-order logic, I again did almost none of the homeworks, skipped half the Iectures, skimmed a couple of the slides, and aced all of the exams.)

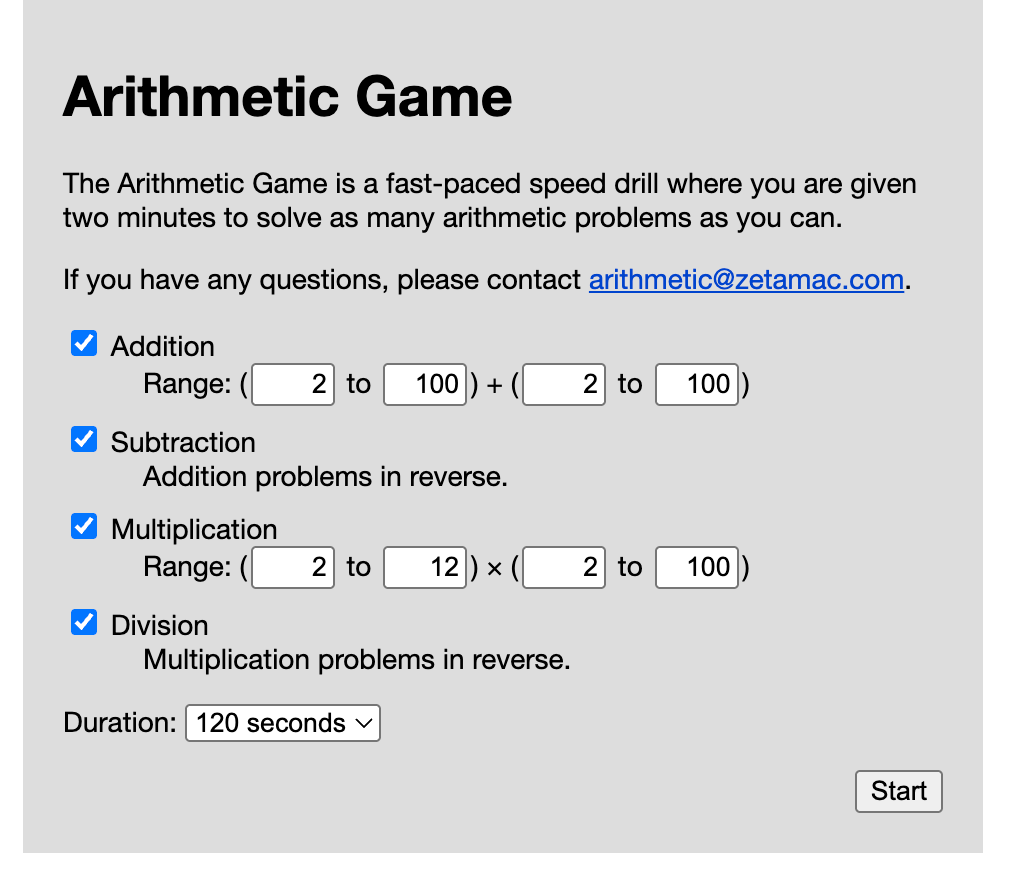
A couple years ago, a friend showed me Zetamac. It’s a “fast-paced speed drill where you are given two minutes to solve as many arithmetic problems as you can.” And it’s surprisingly fun — you’re shown questions like 15+87 or 224÷7, and just have to solve them as quickly as possible. I found doing Zetamac fun, like doing typing speed tests.

At this point in the post, I encourage you to try doing one or two rounds of Zetamac. My guess is that it’ll help you get a sense of the things I discuss below, especially if you happen to be as bad at it is as I was.

With Zetamac’s default settings, I’d typically get a score of 8 or 9. On a great run, I’d get 12 or 14. My best score of ~50 trials over a week or two was 20. My friends were consistently getting 25-30, and occasionally up to 40 or higher.

I knew I was slow, but this was, somehow, simple enough to be clarifying: there was something they had that I didn’t.

II. …but maybe I don’t have to be slow

It was early 2025 that I started reading some of Justin Skycak’s writing. His tone is at times frustratingly self-help-y, condescending, and un-empathetic. And also, at different times, he’s inspiring and enlightening. For examples, look at these pieces.

However: I found his piece on having automaticity in basic arithmetic for learning algebra pretty raw. The piece is short, so consider just giving it a skim. For me, the feeling of some of his characters resonated — that of painfully working through the details of some problem, getting bottlenecked on the slowness of particular subskills (in this case, basic mental arithmetic), giving up in frustration, or just generically not being able to "get" it. That feeling bounced around in my head, and swelled ‘til it hurt.

So in May 2025, I oriented with greater agency to the fact that being slow at math is a problem I could try to solve. What can I do to get faster? Much faster? (Or alternatively: in a future where I become much faster at math, what must have happened?)

Here’s what I did, and how it worked.

III. Straight to the goal

I asked myself “what about just trying to get way faster at mental arithmetic?" For which the straightforward method is just to grind Zetamac, the thing which I was using as a metric. Maybe Goodharting works!

But after ~100 trials, my score was basically not improving. Hmm. Maybe Goodharting doesn’t work after all.

IV. Detour to the goal

I realized that there were so many distinct mental movements in doing a Zetamac trial that each trial wasn't instilling any of them deep enough into my long-term memory. I was drilling "7*13" on one rep, then "396÷6" on another, and a thousand other possible combinations on a thousand different reps. Stuff wasn't adding up accumulating. So I started considering ways to just drill those distinct mental movements directly.

I already had an Anki habit. (Separately, I’d recommend building one yourself — here are some resources I collated on getting started & getting better.) So… what about just making an Anki deck for all of the distinct mental movements that compose a Zetamac trial; then, do Zetamac once I'd mastered those more-basic movements more deeply?

So I did:

• I made a deck that included the twelve times & division table, but also e.g. 2^{2,3,4,10}, 10^{2,3,4,5,6,9,12}, addition with single-digit numbers that add to greater than 10 (e.g. 7+4 or 6+7) & subtraction with the same set of numbers, and a few more basic, distinct mental movements that, when fashioned together in the right way, find you at the answer of a Zetamac question.
• I would review that deck every day. My reviews would look like:
  • Just say the first thing that comes to mind. Don’t “try to make it correct” — just spit out a number.
  • If the number you spat out was correct & said in < 0.5 seconds, mark it “correct.”
  • If the number you spat out was either wrong or said in > 0.5 seconds, mark it “wrong.”
  • If it took me about 0.5 seconds, I’d mark it “hard.”
  • I’d add 5 new cards per day.
  • It’d take me ~10 minutes each day — 1% of my day.

V. It worked

Right now, after six straight months of 2-15m of this exact routine every single day without fail, I consistently score 19-21 on Zetamac. That was the single best score I'd ever accomplished, in my past life. It's now just... average.

And I started seeing a striking difference after just a month or two. All of a sudden, I would sometimes just magically notice that I'd already finished with some simple step of some math problem that would've normally been just a teensy bit of a pain. And then I started skating through more complicated math problems that would've been a horrible annoyance before. Even now, things are still starting to fall before me, walls to rooms I didn't realize I was locked out of, just crumbling with a light touch. And it wasn’t just speed that made a difference — though that did make a difference — but I'm also much more accurate much more often and much more confident in that accuracy, which subsequently makes the whole process was much more enjoyable. These all then feed back into each other.

There’s a great piece by JSomers on why speed matters. I’d recommend reading that piece, it's long and worth it, but since you probably won’t:

• I could do more units of math per unit time, because many of the units of math I was doing went much faster.
• The emotional/mental cost of doing math went down, so I was inclined start practicing math more, and to spend more time on math once starting.
• I felt less struggle while doing math, and so could put less of my effort at the struggle, and more at the math.
• The feedback loops quickened — I could check my results of longer problems more easily, or test a theorem by running a problem with round numbers through my head, or learn a new concept just by doing a few practice problems — which meant that I got better at learning math, more quickly.

Notice, too, that all of the above are positive feedback loops! They don't virtuously feed back positively into each other forever, they'll end, they each only un-bottleneck each other so much, but they help.

I finally understand why people find doing practice problems useful: they seem to skate by on the details of the problem because they’re fluent in the details of the problem — and so they’re able to generalize across those particulars and see the broader patterns, quickly and easily, in the numbers. Learning how matrix multiplication works should be bottlenecked on learning how matrix multiplication works, not on what 8*12 is; but lots & lots of practice multiplying matrices will be a horrible pain in the ass that doesn't contribute to your understanding of matrix multiplication if you're constantly pushing up against how 8*12 is, well, let's see, that's 8 times 10 is 80, plus, uh, that's 8 times 2 is 16, so that's 16 plus... plus, what was it again, 8 times 10 is 80, so that's 16 plus 80, that's 96.

But now, I see "8*12," and "ninety six" will jump into mind before I even realize I've multiplied them. I can just... peacefully continue with the problem. I can spend my effort thinking about how all these elements get manipulated as a matrix, and not how to do third grade multiplication.

VI. Emotional

I want to emphasize how insanely easy this was for me:

• It took me ~10 minutes to make the deck.
• It took me ~2-15 minutes each day to study.
• It takes me 30m-1h once every couple months to prune my deck.

And I now want to emphasize how much of a thorn in my side this has been. Since first grade, it’s caused me to have a confusing love-hate instead of love-love relationship to math, caused me to drop math classes that seemed at-once too easy and too hard for me, and caused me to waste over a thousand hours on homework I otherwise wouldn’t have spent, Fermi estimate in the footnote [1]. And that’s ignoring all of the math that I could’ve done, the years ahead I could’ve skipped, or the other fields I could’ve learned instead.

It feels like I’ve been in a wheelchair my whole life, and that just now I realized that, actually, it took about 10m/day of practice for 5-6 months to be able to walk. I’m angry, but at the same time so incredibly motivated to learn all of the math — and the other fields bottlenecked on a generalist understanding of math — that I haven’t learned yet. But I'm also just generally much more capable: I can do a wide swath of skills that I'm just now realizing were bottlenecked on these more basic ones. For one, I can do so many more Fermi estimates, so much more quickly; deyanu.

If the above resonated with you, consider doing the same routine — I’d be happy to chat with you about it.

[1] I expect the total time I have—and could have—spent getting faster on mental arithmetic to be about 15h (7.5m avg per day for about 4 months, 5-10m typically and occasionally much more than that). I did about 10 years of math through high school after learning basic arithmetic, which translates to about 1-3 thousand hours of math homework. I’d guess that I could’ve spent about 1/2 to 2/3 the time doing the homework that I did, if I had learned basic mental arithmetic to fluency. That translates to about 500-1500 hours of homework saved; the 15 hours spent getting mental arithmetic to fluency is a rounding error.